Inhoudsopgave:
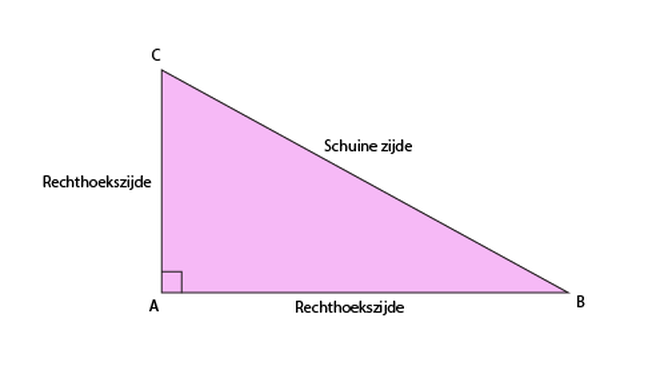
Pythagoras uitleg
De stelling van Pythagoras wilt zeggen dat als je bij een rechthoekige driehoek dat de 2 rechte zijdes bij elkaar opgeteld in kwadraat de schuine zijde is. Oftewel a 2 + b 2 = c 2 . Als je de schuine zijde weet en een rechte zijde dan is de formule C 2 – b 2 = a 2.
Je kan de zijdes op veel manieren uitrekenen.
Manier 1: Tabel
Korte zijde + korte zijde = lange zijde
Zijde zijde in cm Kwadraat
Korte zijde 5 25
Korte zijde____ 6 _ ____ 36____ _ +
Lange zijde 7.8 61
Bij het gebruik maken van een tabel doe je eerst de getallen individueel in kwadraat. De twee korte zijdes tel je bij elkaar op. Dan krijg je de lange zijde in kwadraat. Om de zijde te weten van de lange, oftewel schuine, zijde dan neem je van de lange zijde de wortel. De wortel van 61 is 7.8.
Manier 2
Deze manier is heel kort en hoef je niet zoveel op te schrijven. Bij deze manier vervorm je de formule a 2 + b 2 = c2.
Als je de zijde a wilt weten vervorm je de formule naar de wortel van c 2 – b 2 = a 2.
Als je de zijde b wilt weten dan doe je de wortel van c 2 – a 2 = b 2
Je gebruikt de wortel elke keer omdat je steeds rekent met kwadraten. De stelling van pythagoras kun je alleen gebruiken als je een rechte hoek hebt. Heb je geen rechte hoek dan kun je de zijdes uit rekenen met Tangens, Sinus of cosinus. Wil je de hoeken uitrekenen dan gebruik je Tangens -1, Cosinus -1 en Sinus -1.
Voorbeeld
Rechts zie je de driehoek ABC. B is 5 cm en A is 7 cm.
Reken C uit met de stelling van Pythagoras.
Formule is a 2 + b 2 = c2.
A 2 = 7 2
B 2 = 5 2
C = ?
7 2 + 5 2 = 74
Wortel van 74 is 8.6 cm
Voorbeeld
Van de driehoek DEF is de schuine zijde 8 cm en de korte zijde 4.
Reken de korte zijde uit.
A² = ?
B² = 4
C² = 8
8² – 4 2 = 48
Wortel van 48 is 6.9 cm
Pythagoras oefeningen
Wiscat pabo oefenen
Wil je WisCAT pabo oefenen? Doe dan de WisCAT training. Met onze WisCAT training kun je levenslang veel gebruikte onderdelen van de rekentoets oefenen. Op deze manier zorg je ervoor dat je automatisch beter gaat presteren op de rekentoets, door middel van herkenning van de manier van vraagstelling en door het oefenen van de stof op de juiste manier! Klik hier om verder te gaan naar de WisCAT training.





